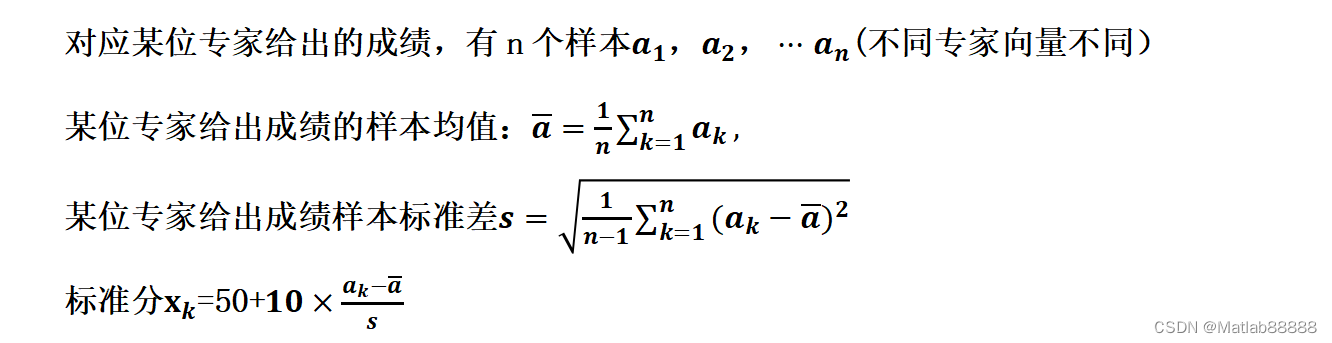💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
离散傅里叶变换(Discrete Fourier Transform,DFT)作为一种基本工具广泛应用于工程、科学以及数学领域。例如,通信信号处理中,常用DFT实现信号的正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)系统的时频域变换(见图1)。另外在信道估计中,也需要用到逆DFT(IDFT)和DFT以便对信道估计结果进行时域降噪(见图2)。
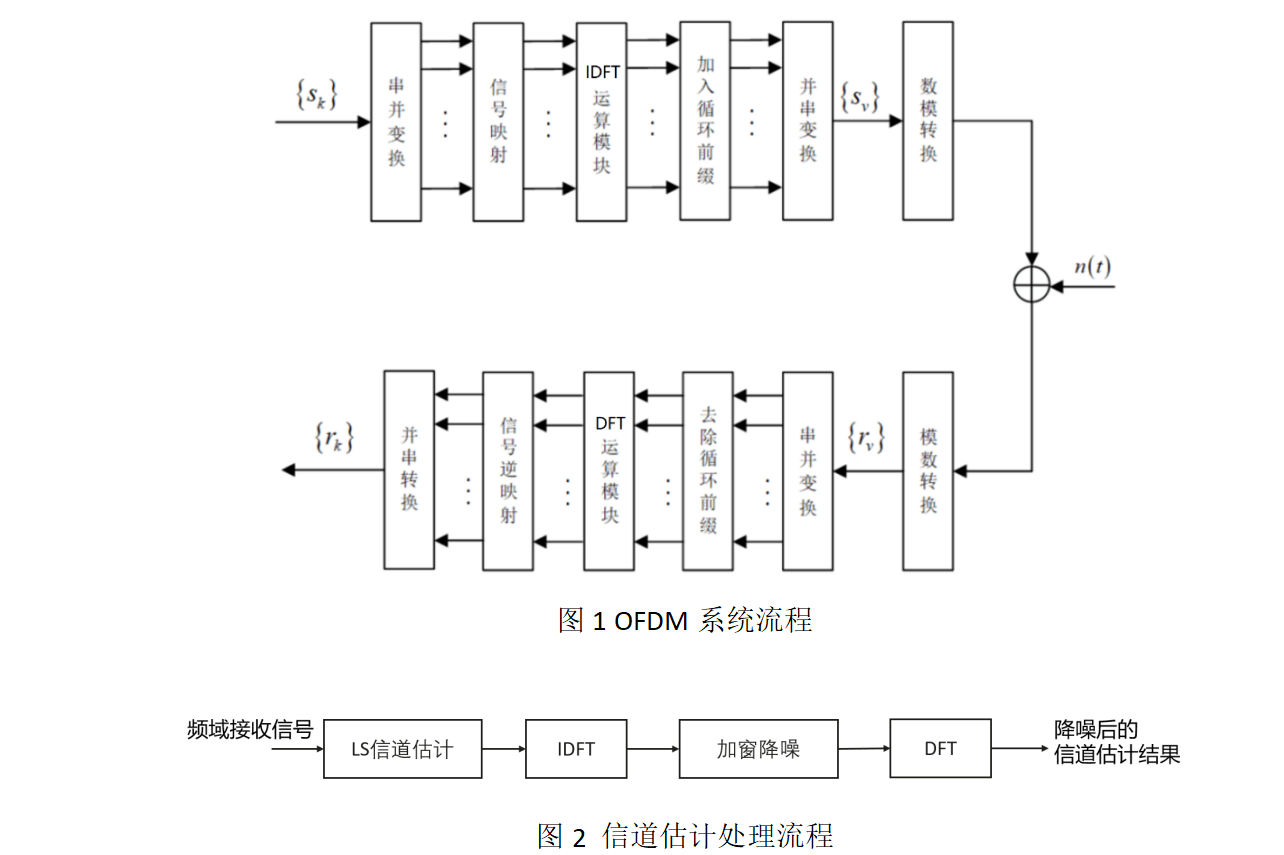
在芯片设计中,DFT计算的硬件复杂度与其算法复杂度和数据元素取值范围相关。算法复杂度越高、数据取值范围越大,其硬件复杂度就越大。目前在实际产品中,一般采用快速傅里叶变换(Fast Fourier Transform,FFT)算法来快速实现DFT,其利用DFT变换的各种性质,可以大幅降低DFT的计算复杂度(参见[1][2])。然而,随着无线通信技术的演进,天线阵面越来越大,通道数越来越多,通信带宽越来越大,对FFT的需求也越来越大,从而导致专用芯片上实现FFT的硬件开销也越大。为进一步降低芯片资源开销,一种可行的思路是将DFT矩阵分解成整数矩阵连乘的形式。
📚2 详细数学模型及题目、数据
链接:https://pan.baidu.com/s/1xBW-DjaT_Jt2jfrW_CUPLw
提取码:l662
--来自百度网盘超级会员V4的分享
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
- James W. Cooley and John W. Tukey, An Algorithm for the Machine Calculation of Complex Fourier Series, Mathematics of Computation, vol. 19, no. 90, pp. 297-301, 1965. DOI:10.2307/2003354.
- K. R. Rao, D. N. Kim, and J. J. Hwang, Fast Fourier Transform: Algorithms and Applications, Springer, 2010. (中译本:快速傅里叶变换:算法与应用,万帅,杨付正译,机械工业出版社,2012.)
- Viduneth Ariyarathna, Arjuna Madanayake, Xinyao Tang, Diego Coelho, et al, Analog Approximate-FFT 8/16-Beam Algorithms, Architectures and CMOS Circuits for 5G Beamforming MIMO Transceivers, IEEE Journal on Emerging and Selected Topics in Circuits and Systems, vol. 8, no. 3, pp. 466-479, 2018. DOI: 10.1109/JETCAS.2018.2832177.
🌈4 Matlab代码及思路实现
相关文章
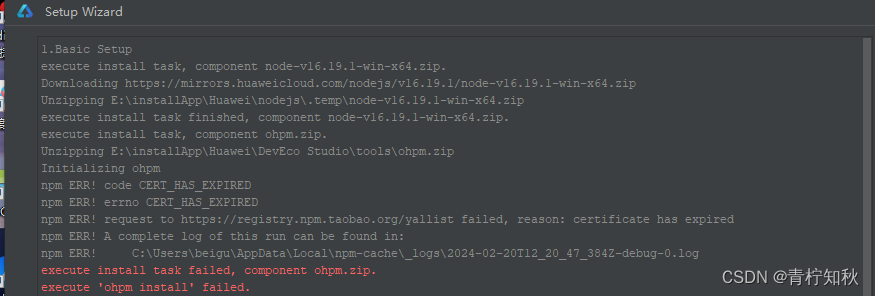
harmony 鸿蒙系统学习 安装ohpm报错 ohpm install failed
找原因,首先,通过查看文件,先看软件的使用node的配置,发现config用的是 .npmrc文件,去c盘找到对应文件打开看看。确实是,这里的镜像不对。(网上很多攻略要求你卸载以前的node或者卸载这个刚安装的软件,再重装,其实不需要这么麻烦。)
编程日记 2024/02/21 09:47:51
HarmonyOS应用开发者基础认证考试答案
B. 通过"$r(‘app.type.name’)"的形式引用应用资源,app代表是应用内resources目录中定义的资源,type代表资源类型(或资源的存放位置)。5.在Column和Row容器组件中,justifyContent用于设置子组件在主轴方向上的对齐格式,alignItems用于设置子组件在交叉轴方向上的对齐格式。E. 属性方法:用于组件属性的配置,统一通过属性方法进行设置,如fontSize()、width()、height()、color() 等。
编程日记 2024/02/04 10:02:02
HarmonyOS 页面page间元素转场动画
这里 id我们还写没写 然后 第二个参数 我们设置 动画 2000毫秒 就是两秒执行完。但是 目前 我们跳转是没有什么动画 看不出什么特别明显的动态效果的。我们可以给第一个 和第二个界面 image图片组件都加上如下代码。然后 还有一个问题 我们需要的是 这个图片一个慢慢变大的效果。此时 我们点击图片 它就会跳到我们 AppView 来了。第二个 是我们属性的 json 类型的动画配置参数。我们第二个界面的 image组件也要对应加上。这里 我们写的基本和第一个界面一模一样的结构。
编程日记 2024/01/19 21:10:56
鸿蒙Harmony-列表组件(List)详解
不要和别人比生活,每个人阶段不同,追求不同,活法自然也不同。只要今天的你能比昨天的你快乐一点点,那你就是自己人生赢家。
编程日记 2024/01/18 13:22:22
HarmonyOS4.0系统性深入开发19进程模型概述
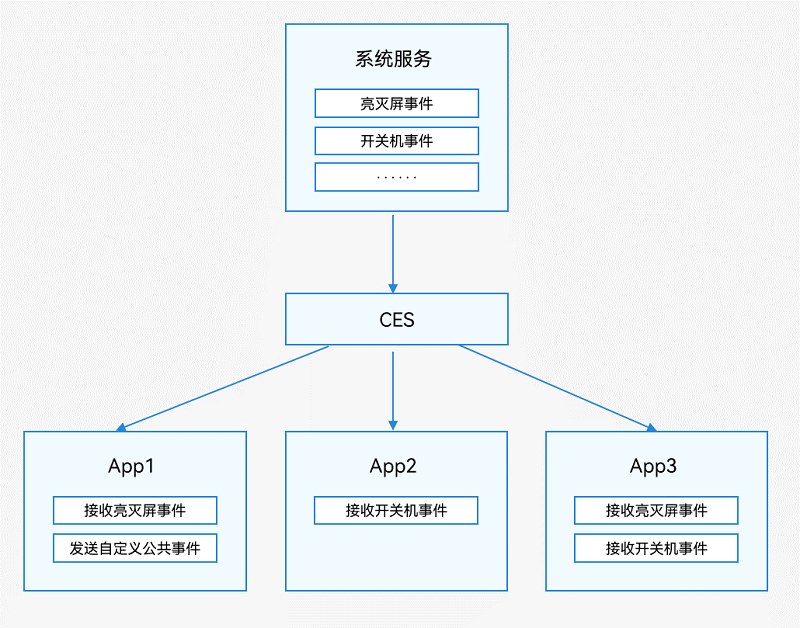
HarmonyOS通过CES(Common Event Service,公共事件服务)为应用程序提供订阅、发布、退订公共事件的能力。公共事件从系统角度可分为:系统公共事件和自定义公共事件。系统公共事件:CES内部定义的公共事件,只有系统应用和系统服务才能发布,例如HAP安装,更新,卸载等公共事件。目前支持的系统公共事件详见系统公共事件列表。自定义公共事件:应用自定义一些公共事件用来实现跨进程的事件通信能力。公共事件按发送方式可分为:无序公共事件、有序公共事件和粘性公共事件。
编程日记 2024/01/15 09:47:24
【HarmonyOS】深入了解 ArkUI 的动画交互以提高用户体验
从今天开始,博主将开设一门新的专栏用来讲解市面上比较热门的技术 “鸿蒙开发”,对于刚接触这项技术的小伙伴在学习鸿蒙开发之前,有必要先了解一下鸿蒙,从你的角度来讲,你认为什么是鸿蒙呢?它出现的意义又是什么?鸿蒙仅仅是一个手机操作系统吗?它的出现能够和Android和IOS三分天下吗?它未来的潜力能否制霸整个手机市场呢?抱着这样的疑问和对鸿蒙开发的好奇,让我们开始今天对ArkUI动画操作的掌握吧!
编程日记 2024/01/09 09:45:28
【HarmonyOS】鸿蒙开发简介与项目基础配置演示
从今天开始,博主将开设一门新的专栏用来讲解市面上比较热门的技术 “鸿蒙开发”,对于刚接触这项技术的小伙伴在学习鸿蒙开发之前,有必要先了解一下鸿蒙,从你的角度来讲,你认为什么是鸿蒙呢?它出现的意义又是什么?鸿蒙仅仅是一个手机操作系统吗?它的出现能够和Android和IOS三分天下吗?它未来的潜力能否制霸整个手机市场呢?
编程日记 2024/01/01 22:00:40
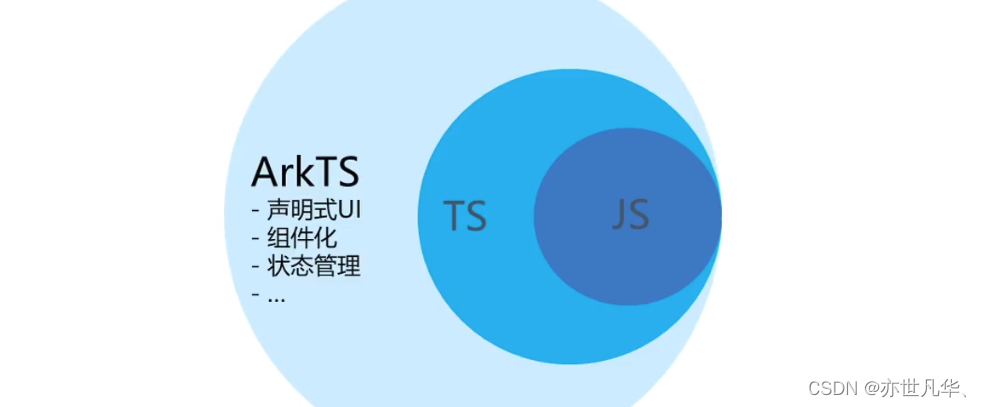
【HarmonyOS】ArkTS语言介绍与组件方式运用
自定义组件自定义函数:自定义函数可以将烦长的代码单独抽离出一个函数当中,然后在原位置调用我们设置的函数即可,自定义函数可以定义在全局或组件内,如下:@Styles装饰器@Extend装饰器// 继承模式,只能写在全局。
编程日记 2024/01/01 10:01:42
移动开发新的风口?Harmony4.0鸿蒙应用开发基础+实践案例
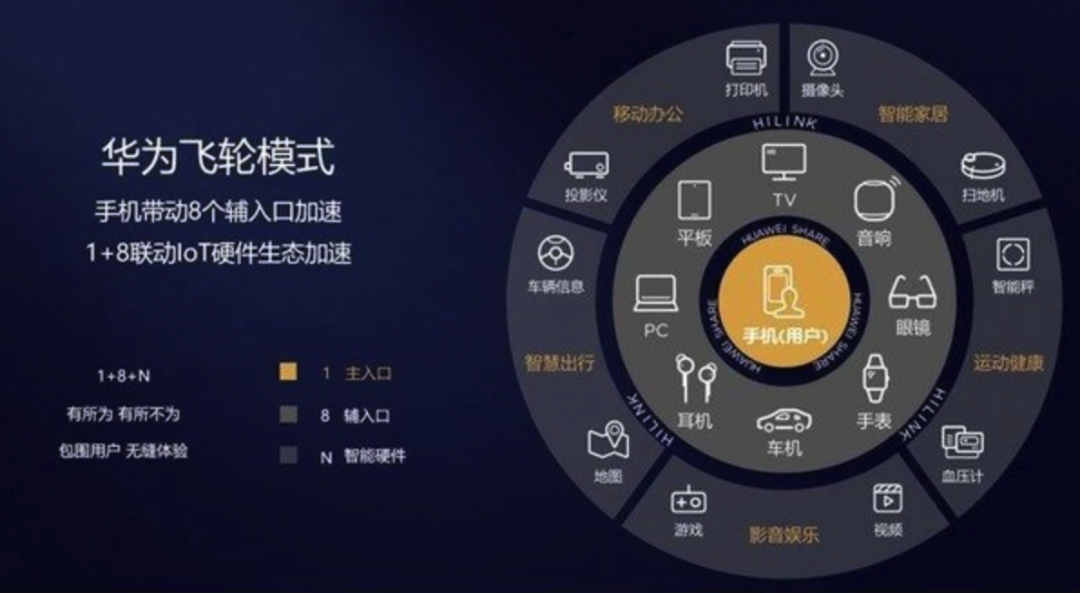
HarmonyOS 是啥?HarmonyOS 是华为新一代的智能终端操作系统,为不同设备的智能化、互联与协同提供了统一的语言。带来简洁、流畅、连续、安全可靠的全场景交互体验。
编程日记 2023/12/27 17:53:06
鸿蒙应用开发 常用组件与布局
HarmonyOS ArkUI 提供了丰富多样的 UI 组件,您可以使用这些组件轻松地编写出更加丰富、漂亮的界面。在本篇 Codelab 中,您将通过一个简单的购物社交应用示例,学习如何使用常用的基础组件和容器组件。本示例主要包含:“登录”、“首页”、“我的”三个页面。
编程日记 2023/12/24 20:08:33
【2023华为杯A题】WLAN网络信道接入机制建模(代码、思路.....)
AP给STA发送数据叫作下行方向,反之是上行方向,本文将AP和STA统称为节点,每个节点的发送和接收不能同时发生。家庭或宿舍等单BSS场景中,STA距离AP较近,RSSI较强,互听,假设理想信道,不会因信道质量差而丢包,只有在2个及以上STA同时发送数据时导致碰撞而丢包。(2)随机回退:信道空闲时,可能有多个节点准备好了数据,为避免碰撞,节点从[0, CW-1]的均匀分布选取一个随机数作为回退数,等待该回退数个时隙长度slotTime(9μs),随机回退时段时长为回退数乘以slotTime。
AI专题 2023/09/23 23:18:07
【 2023华为杯C题】大规模创新类竞赛评审方案研究(思路、代码......)
现在创新类竞赛很多,其中规模较大的竞赛,一般采用两阶段(网评、现场评审)或三阶段(网评、现场评审和答辩)评审。创新类竞赛的特点是没有标准答案,需要评审专家根据命题人(组)提出的评审框架(建议)独立评审。所以,对同一份作品,不同评委的评分可能存在较大差异。事实上,当竞赛规模大,评委的人数众多时,极差(定义见附件1)大的问题更为突出。显然,简单地依据多位评委评分的总和进行排序并不是创新类竞赛评审的好方案。因此,探讨大规模创新类竞赛评审方案的公正性、公平性和科学性具有深远意义。
AI专题 2023/09/23 23:17:58